Krzysztof Z Sokalski
Czestochowa University of Technology, Poland
Title: Scaling a way for revealing self-similar features of materials and new applications
Biography
Biography: Krzysztof Z Sokalski
Abstract
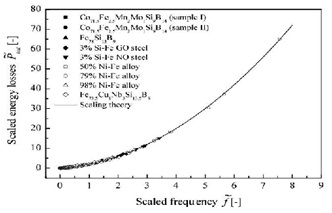
Certain features of certain materials are self-similar. This phenomenon is recognizable by scaling of measurement data corresponding to the considered self-similar feature. To perform scaling we apply notion of homogenous function in general sense. For two independent variables such a function reads P(f,B)=Bβ F(f/Bα), where P is a considered magnitude, α and β are scaling exponents, F(∙) is an arbitrary continuous function, where α, β and F(∙) have to be determined by the measurement data. Definition of P(f,B) enables us to transform all characteristics P(f,B) to the one universal function of the one variable: P(f,B)/ Bβ =F(f/Bα ). This effect is so called the data collapse and can be applied for comparison of measurement data measured in different laboratories, which enable us to estimate quality of each laboratory series. Another application of the data collapse is compression of large experimental data. If the considered data are produced by a self-similar system then one can store them in a form of continuous curve. The data collapse enables us to introduce an absolute dimensionless characteristic: 
1), where P and f are dimensionless P and f, respectively. This characteristic divides { P, f } space into the two independent subspaces of materials’ characteristics.
Finally, the scaling supplemented by pseudo-equation of states plays basic role in creation of algorithms for designing of modern materials.
The presented results base on experimental data of Soft Magnetic Materials and Soft Magnetic Composites. Where, P(f,B) is density of power loss, f is frequency of the field’s modulation and B is maximum of magnetic induction. One can apply this simple mathematics to any self-similar object. However, ultimately one must say that the degree of success achieved when applying the scaling depends on the property of the data. The data must obey the scaling.